Dda Circle Drawing Algorithm Geeks for Geeks

Line Generation Algorithm

A line connects two points. It is a bones element in graphics. To draw a line, y'all need two points between which you tin can depict a line. In the following three algorithms, we refer the one signal of line equally $X_{0}, Y_{0}$ and the 2nd point of line as $X_{1}, Y_{1}$.

DDA Algorithm

Digital Differential Analyzer (DDA) algorithm is the simple line generation algorithm which is explained step past step hither.

Step i − Get the input of two end points $(X_{0}, Y_{0})$ and $(X_{1}, Y_{1})$.

Step two − Summate the divergence between two finish points.

dx = X_i          - X₀          dy = Y_one          - Y₀

Step three − Based on the calculated difference in stride-ii, y'all need to identify the number of steps to put pixel. If dx > dy, then you lot need more steps in 10 coordinate; otherwise in y coordinate.

if (absolute(dx) > absolute(dy))    Steps = absolute(dx); else    Steps = accented(dy);

Step four − Calculate the increase in x coordinate and y coordinate.

Xincrement = dx / (float) steps; Yincrement = dy / (float) steps;

Step 5 − Put the pixel past successfully incrementing x and y coordinates accordingly and consummate the cartoon of the line.

for(int v=0; five < Steps; five++) {    ten = x + Xincrement;    y = y + Yincrement;    putpixel(Round(x), Round(y)); }

Bresenham's Line Generation

The Bresenham algorithm is another incremental scan conversion algorithm. The large advantage of this algorithm is that, it uses only integer calculations. Moving beyond the x axis in unit of measurement intervals and at each step choose betwixt two unlike y coordinates.

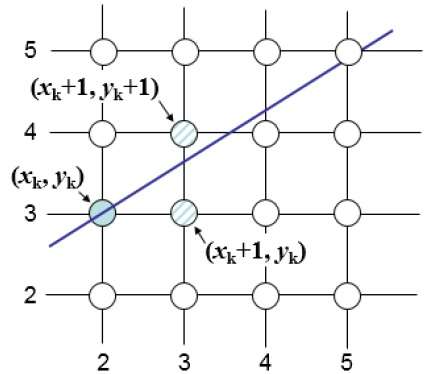
For instance, every bit shown in the following analogy, from position (ii, 3) you lot need to choose between (3, iii) and (3, four). You would similar the bespeak that is closer to the original line.

Bresenham's Line Generation

At sample position $X_{k}+1,$ the vertical separations from the mathematical line are labelled as $d_{upper}$ and $d_{lower}$.

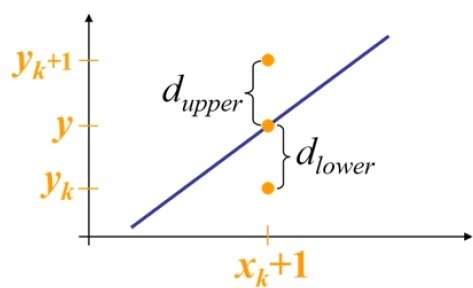
dupper and dlower

From the above analogy, the y coordinate on the mathematical line at $x_{k}+ane$ is −

Y = yard($X_{1000}$+1) + b

Then, $d_{upper}$ and $d_{lower}$ are given as follows −

$$d_{lower} = y-y_{k}$$

$$= chiliad(X_{chiliad} + i) + b - Y_{k}$$

and

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{g} + 1 - m (X_{k} + 1) - b$

You tin use these to brand a simple decision nigh which pixel is closer to the mathematical line. This simple decision is based on the difference between the two pixel positions.

$$d_{lower} - d_{upper} = 2m(x_{yard} + 1) - 2y_{k} + 2b - 1$$

Allow us substitute yard with dy/dx where dx and dy are the differences between the cease-points.

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - ane)$$

$$ = 2dy.x_{1000} - 2dx.y_{k} + 2dy + 2dx(2b-i)$$

$$ = 2dy.x_{yard} - 2dx.y_{thousand} + C$$

And so, a determination parameter $P_{k}$ for the kth step along a line is given by −

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{yard} + C$$

The sign of the decision parameter $P_{k}$ is the same as that of $d_{lower} - d_{upper}$.

If $p_{k}$ is negative, so cull the lower pixel, otherwise choose the upper pixel.

Remember, the coordinate changes occur forth the x axis in unit of measurement steps, so you tin practise everything with integer calculations. At stride k+1, the decision parameter is given as −

$$p_{k +1} = 2dy.x_{yard + 1} - 2dx.y_{k + 1} + C$$

Subtracting $p_{k}$ from this we get −

$$p_{thou + 1} - p_{yard} = 2dy(x_{k + i} - x_{k}) - 2dx(y_{thou + 1} - y_{k})$$

Merely, $x_{g+1}$ is the same as $(xk)+1$. So −

$$p_{k+1} = p_{grand} + 2dy - 2dx(y_{k+1} - y_{grand})$$

Where, $Y_{k+one} – Y_{chiliad}$ is either 0 or 1 depending on the sign of $P_{k}$.

The start conclusion parameter $p_{0}$ is evaluated at $(x_{0}, y_{0})$ is given as −

$$p_{0} = 2dy - dx$$

Now, keeping in listen all the above points and calculations, here is the Bresenham algorithm for gradient m < i −

Step ane − Input the 2 stop-points of line, storing the left end-point in $(x_{0}, y_{0})$.

Step 2 − Plot the point $(x_{0}, y_{0})$.

Step 3 − Calculate the constants dx, dy, 2dy, and (2dy – 2dx) and get the first value for the conclusion parameter every bit −

$$p_{0} = 2dy - dx$$

Step 4 − At each $X_{k}$ forth the line, starting at m = 0, perform the following examination −

If $p_{k}$ < 0, the next point to plot is $(x_{k}+1, y_{thousand})$ and

$$p_{k+i} = p_{k} + 2dy$$ Otherwise,

$$(x_{thousand}, y_{k}+1)$$

$$p_{g+ane} = p_{grand} + 2dy - 2dx$$

Step 5 − Echo footstep four (dx – one) times.

For yard > 1, find out whether you need to increase x while incrementing y each time.

After solving, the equation for decision parameter $P_{thou}$ will be very like, just the x and y in the equation gets interchanged.

Mid-Point Algorithm

Mid-point algorithm is due to Bresenham which was modified by Pitteway and Van Aken. Assume that you have already put the betoken P at (x, y) coordinate and the gradient of the line is 0 ≤ one thousand ≤ 1 as shown in the following illustration.

Now you need to decide whether to put the next point at E or N. This tin can exist chosen by identifying the intersection betoken Q closest to the point N or East. If the intersection point Q is closest to the point N then North is considered as the next point; otherwise Due east.

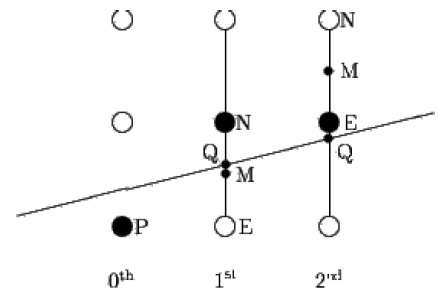
Mid-Point Algorithm

To determine that, start calculate the mid-indicate M(x+one, y + ½). If the intersection bespeak Q of the line with the vertical line connecting East and Northward is below 1000, and then have E as the next point; otherwise take N as the next point.

In order to cheque this, nosotros demand to consider the implicit equation −

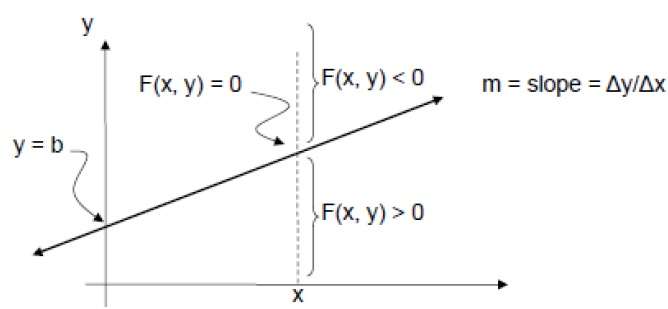
F(x,y) = mx + b - y

For positive m at any given X,